Analysis of Bioassays

Recently, I went through the woods with one of my younger kids and it was amazed by the various colors of different mushrooms. Kids tend to touch almost everything and sometimes even to put into their mouth what they see. However, for certain mushrooms this might not be such a good idea and I taught my kid that some mushrooms and other subtances are poisonous. For the next few weeks it kept asking for the toxicity of almost everything on our dinner table, like: “Papa, is salt poisonous?”. As a scientist I used to answer: “Yes, but just at a very high dose.” Then I had to explain what Paracelsus already claimed in the 16th century:

“Wenn ihr jedes Gift wollt recht auslegen, was ist, das nit Gift ist? Alle Ding sind Gift und nichts ohn Gift. Allein die Dosis macht, dass ein Ding kein Gift ist.”
Freely translated: “If you want to interpret every poison correctly, what is there that is not a poison? All things are poison and nothing is without poison. The dose alone makes a thing a poison.”
Paracelsus (1538)

Let’s stick to the salt example (my kid asked about table salt, i.e. sodium chloride). Let’s assume we’d put groups of rats on diet with the intake of various doses of sodium chloride added to their food. Say we run this experiment several weeks and look at the number of deaths within the different rat groups after a certain time point. Rats that had a very high intake of sodium chloride will likely be dead after the time period, while those with a lower intake will likely not have died. Plotting the portion of death rats versus the (log) dose of the sodium chloride will result in a dose-response curve and the assay just described is an example of a bioassay with quantal response data. I will explain in detail below what that actually means.

According to Finney (1947) a biological assay (bioassay) can be defined as follows (my comments in square brackets below):

“The term biological assay, in its widest sense, should be understood to mean the measurement of the potency of any stimulus, physical, chemical [sodium chloride in our case] or biological, physiological or psychological, by means of the reactions [dead or alive in our case] which it produces in living matter [rats in our case].”
D.J. Finney, Probit Analysis – A Statistical Treatment of the Sigmoid Response Curve, 1947, Cambridge University Press

Finney’s definition makes clear that bioassays are very diverse by means of what type of stimulus is applied and by means of what the reaction or response might look like that the stimulus induces. It might also become clear that bioassays are performed in various fields of science ranging from ecotoxicology to pharmacology. Of similar diversity can be the data resulting from those bioassays as will be discussed below.

Bioassays are typically classified as direct assays, where the dose needed to induce a fixed response (e.g. death of an organism) is directly measured. The dose itself is the random variable. In terms of our salt example we might increase the sodium chloride concentration in the blood of a rat until its heart stops beating. With indirect assays the doses are fixed and the responses are the random variables. While direct assays produce binary output data, indirect assays can be either produce continuous or binary data and result in dose-response curves that need to be analyzed in an appropriate fashion.

In the following, we will focus on the analysis of indirect bioassays and start with introducing dose-response curves and their corresponding mathematical models.

A closer look at dose-response curves

Let’s assume we are working for a pharma company producing drugs for reducing blood pressure. Let’s further assume we developed a new drug candidate by changing a chemical side-group. That drug seems promising against our reference standard (substance). Look at the following graph:

The dose-response curve of the reference substance is shown in blue while that of our new drug candidate is shown in black. In fact the latter is like a left-shifted version of dose-response curve of our reference standard. This is typically a reasonable hint that both drugs act in a similar way. The shift to the left indicates that our new drug candidate requires a lower dose to induce the same effect as our reference standard. One says that our drug candidate has a higher potency. That’s good, as less subtance needs to be produced and side-effects are less likely. The dose-response curves shown above are of sigmoid shape which is quite common in practice. By the way, the shift along the log(Dose) axis between the two curves denotes the so-called log relative potency which we’ll discuss in more detail later on.

In the example above, the responses are contiuous as the blood pressure, or a ratio thereof, is a continuous random variable with a continuous error distribution (often the normal distribution). In the life sciences and from what I personally experience, I’d say that the so-called four-parameter logistic (4PL) model is most commonly used to model dose-response data in practice:

$f(\vec{x},b,c,d,e) = c+\frac{d-c}{1+\exp\left(b\cdot(\log(\vec{x}) - \log(e)) \right)}$

Herein $\vec{x}$ denotes the vector of doses and $b,c,d,e$ denote the Hill-Slope, the lower and upper asymptote of the dose-response curve and the effective dose 50 (ED₅₀). $b,c,d,e$ are model parameters being estimated within the curve-fitting procedure (more details below).

The 4PL model is of sigmoid shape and symmetric around its inflection point. However, sometimes it might be required to fit an assymetric sigmoid to the data. This can be achieved by taking into account an assymetry parameter $a$ in the denominator of the aforementioned equation:

$f(\vec{x},b,c,d,e) = c+\frac{d-c}{\left(1+\exp\left(b\cdot(\log(\vec{x}) - \log(e)) \right) \right)^a}$

Both models are displayed in the following figure. The log effective dose 50 is at -5 as indicated by the vertical dashed line at the corresponding $\log(x)$ value. Except for the assymetry parameter (which is $a=0.2$ for the 5PL curve and $a=1$ for the 4PL model) the fit model parameters are identical.

Sometimes nested models of the 4PL are used such as the three-parameter (i.e. c=0) or two-parameter logistic function (i.e. c=0, d=0):

$f(\vec{x},b,e) = \frac{1}{1+\exp\left(b\cdot(\log(\vec{x}) - \log(e)) \right)}$

The latter model is highly important when fitting binary response data (more details below). Of course there are more fit models but talking about all of them is out of the scope of this blog post.

The ED₅₀ is the dose of a compound required to produce 50 % of the maximal response. It is an important parameter and is related to the aforementioned potency. The lower the ED₅₀ of a compound, the higher its potency.

While we focus on parametric fit models here, I don’t want to keep from you the fact that there also exist non-parametric methods to analyze dose-response curves, such as the Spearman-Kärber method mentioned in another blog post.

Estimation of fit model parameters

Fitting a model to dose-response data requires two key decisions to make:

What shall the model function 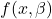$f(x,\beta)$ look like?
What distributional assumption do we make for the dose-response data?

The first decision is clear. You need to choose the functional form of the model. Maybe one of those discussed above. In practice the decision is often anticipated by the assay provider or by literature search. The second decision sounds a bit abstruse. It means that due to the fact that the responses are random variables, they follow some probability distribution. For continuous data this is often the normal distribution, but others like the log-normal are common, too. For quantal data this is often the binomial distribution. In other disciplines, e.g. for counting data, the Poisson distribution is the distribution of choice.

Procedures for estimating the fit model parameters need to take these two ingredients into account.

Maximum likelihood estimation and nonlinear least-squares

In fact, (nonlinear) least-squares (LS) and maximum likelihood (ML) parameter estimation are related, i.e. the LS approach is basically a special case of the ML approach assuming that the distribution $p([y_1,\dots,y_n]|\beta)$ of the noise associated with experimental measurements is sufficiently well described by a normal probability distribution function with zero mean and some standard deviation $\sigma$ .

$p([y_1,\dots,y_n]|\beta) = \prod_{i=1}^{n} \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(y_i-f(x_i,\beta))^2}{2\sigma^2} \right)$

Herein, $[y_1,\dots,y_n]$ denotes vector of response values $y_i$ , $f(x_i,\beta)$ the value of the dose-response model at (log) dose $x_i$ , and parameter vector $\beta$ . $\sigma$ denotes the standard deviation of the scatter. The noise corresponds to the difference $y_i-f(x_i,\beta)$ in the numerator of the exponential function. p([y_1,\dots,y_n]|\beta) is in fact the likelihood function.
We can now also see from the equation above, that for some dose $x$ the corresponding response values $y$ are distributed around $f(x,\beta)$ , the mean of $y$ .

When $p(y_i|\beta)$ is not a normal distribution, but, for instance, a binomial distribution, we are not in the least-squares regime anymore and then other methods such as ML estimation need to be applied to estimate the corresponding model parameters.

By the way, it is relatively easy to show how the likelihood expression $p([y_1,\dots,y_n]|\beta)$ from above reduces to the well-known least-squares expression (i.e. the sum of squared errors):

$L = \sum_{i=1}^{n} w_i \left(y_i-f(x_i,\beta) \right)^2$

where I have also included weights $w_i$ that are often simply $w_i=1$ for all $i$ but can be different from 1, too. In this case it is a weighted least-square (see also this blog post) including methods of robust regression. I’ve used the letter $L$ to indicate that it is the log-likelihood. To reach at the least-squares expression $L$ above, take the natural logarithm of the likelihood $p([y_1,\dots,y_n]|\beta)$ and multiply by $-1$ . Ignore the prefactor of the likelihood and the constant $\sigma$ (being unimportant for the parameter estimation in [unweighted] least-squares) and you are at the sum of squared errors expression shown in the last equation.

Did you know?
The ML and LS approach can both be derived with by Bayes Theorem by assuming a constant prior. The LS approach makes further simplifying assumptions on the likelihood that finally reduces to the well-known sum of squared errors notation of least-squares.

Dose-response curves are often fitted within the framework of generalized linear models (GLM) including Logitstic, Probit, as well as 4PL regression. See also the blog post on logistic regression as well as on the analysi of excess mortality data.

Start with good initial guess values (IG) for the model parameters

To estimate the fit model parameters, you need to solve an optimization problem, i.e. by minimizing the (weighted) sum of squared errors or the negative log-likelihood by varying the fit model parameters given the data. This requires an iterative procedure such as a Levenberg-Marquart algorithm or a Simplex-based method like the one proposed by Nelder and Mead. In any case, good initial guess values of the fit model parameters are required to ensure the algorithm doesn’t get stuck in a local minimum but approaches the global minimum resulting in the optimal solution.

A conventional IG value for the lower asymptote of the 4PL model is to take the value of the minimum response. Accordingly, the IG value for the upper asymptote is often set to the maximum of the response values. For the Hill slope a common IG value is either -1 if the response value at the maximum dose minus the response value at the minimum dose is negative (i.e. the dose-response curve is falling) or the Hill slope is set to 1 if the response value at the maximum dose minus the response value at the minimum dose is positive (increasing dose response curve). Finally, the log(dose) value corresponding to the mean of the minimum and maximum response, is often chosen as initial guess value for the log(ED50).

The five-parameter model (5PL) is more difficult to fit than the 4PL model as the asymmetry parameter $a$ , the Hill slope $b$ and the (log) ED50 $e$ are interwined which means that fit model parameters can be wildly changed (by the fit algorithm) without changing the sum of squared error very much. The fit curve, however, might look very different in places where there are no data (see also this website). We say the optimization problem is ill-conditioned. So, being able to get a proper fit with the 5PL model at all, requires good quality of data and enough data points covering the whole range of the underlying dose-response curve (asymptotes and transition region). But even then, good intial guess values are mandatory. An increasing dose-response curve will have its steepest ascent near the upper asymptote if $a<1$ and near the lower asymptote if $a>1$ . It is the other way around for a decreasing dose-response curve. So it is worth looking at the asymmetric dose-response data first to set good initial guess values for the fit parameters.

Another “trick” that can help to get more reliable fit model parameters is to set lower and upper bounds. For example, if you are confident that $a<1$ for an increasing dose-response data, you should not allow the asymmetry parameter $a$ to vary freely between $-\infty < a < \infty$ , but choose a more confined interval of say $0.1 < a < 1$ .

Estimate relative potencies from multiple dose-response curves

Estimating relative potencies from two or more dose-response curves is an important task in the drug-developing pharma industry. Given a drug A and a drug B used to create two dose-response curves, the relative potency $\rho$ can be estimated by:

$\rho = \frac{ED_{50}^A}{ED_{50}^B}$

Typicall $A$ is some refernce substance (drug) and $B$ some test substance (e.g. an improved drug). If $\rho > 1$ , the drug $B$ has a higher potency than drug $A$ and reaches similar responses at lower doses. On the other hand, if $\rho < 1$ the drug $B$ has a lower potency than drug $A$ . For parallel dose-response curves one could also calculate $\rho$ by using a different $ED_{\gamma}$ (e.g. with $\gamma=20$ or $\gamma=80$ . Proving parallelism is an important step before estimating relative potencies for bioassays. In addition, other validation criteria need to be verified first e.g. as is shown in the US- and European Pharmacopeia. Parallelism for two 4PL dose-response curves typically means they share the same asymptotes and the same Hill slope. To check for parallelism one imposes parallelism on two 4PL dose-response curves by sharing the Hill slope and the lower and upper asymptotes when fitting the corresponding data. Subsequently, the two data sets are fitted independently having their own Hill slope and asymptotes. An ANOVA approach is then used to test whether including more fit parameters in the latter case significantly improved the fit or not. If not, the curves can be considered parallel (the corresponding $p$ -value for “non-parallelism” is above the significance level $\alpha=0.05$ ). There are typically two more criteria that should be met for a bioassay to be valid, i.e the fit model needs to have no significant lack-of-fit (also called non-linearity) and the regression shall be significant at all (the corresponding $p$ -value shall be below $\alpha=0.05$ ). When dealing with 5PL models, the assymetry parameter is additionally shared between the two data sets for the constrained model.

Relative potency assays are by no means limited to continuous data and to 4PL models, but can also be based on quantal data. The validity criteria are essentially the same as those mentioned above. As long as all validity criteria are fullfilled, the relative potency can be estimated by the formula shown above.

The US Pharmacopeia suggests to apply equiavalence testing on the fit model parameters of the unconstrained model. E.g. for the 4PL model the ratio of the Hill slopes and its confidence interval shall be compared against an equivalence interval. The same shall be done for the lower and upper asymptote, respectively. When all the ratios arer close to 1 and their respective confidence intervals are fully contained within the pre-defined equivalence intervals, the dose-response curves are said to be sufficiently similar and subsequently the relative potency can be estimated from the constrained model.

Please note that some bioassays result in linear dose-response data (often after log-transformation of the responses) instead of sigmoid data. In these cases the data is fitted by a linear model having intercept $\beta_0$ and slope $\beta_1$ as fit model parameters:

$f(x,\beta) = \beta_0 + \beta_1 x$

For two parallel-lines the log(relative potency) is estimated by:

$\log(\rho) = \frac{\beta_0^{\text{T}}-\beta_0^{\text{S}}}{\beta_1}$

where $\beta_1$ denotes the common slope and $\beta_0^{\text{T}}$ and $\beta_0^{\text{S}}$ the intercepts for the test preparation and standard preparation, respectively.

These assays are typically called parallel-line assays and the analysis itself is called parallel-line analysis (PLA). As described in the European Pharmacopeia, sigmoid dose-response curves can be linearized and thus, the term PLA is not necessary limited to the linear model. However, you’ll sometimes see the term parallel-curve analysis for the potency estimation of non-linear dose-response data.

A closer look at dose-response curves

Estimation of fit model parameters

Maximum likelihood estimation and nonlinear least-squares

Start with good initial guess values (IG) for the model parameters

Estimate relative potencies from multiple dose-response curves

Dr. Mario Schneider

Leave a Reply Cancel reply

Data analysis for scientists,
engineers and practitioners

A closer look at dose-response curves

Estimation of fit model parameters

Maximum likelihood estimation and nonlinear least-squares

Start with good initial guess values (IG) for the model parameters

Estimate relative potencies from multiple dose-response curves

Dr. Mario Schneider

You Might Also Like

Spearman-Kärber analysis and the Creutzfeld-Jakob disease

Logistic regression in vaccine testing

Leave a Reply Cancel reply