Recently, Microsoft introduced the so-called LAMBDA function allowing users to define custom Excel functions. The concept of user-defined functions in Excel is not new. However, in the past these had to be coded in VBA first and then made available as corresponding functions in Excel in a rather tedious way. The corresponding Excel files were macro files (extension: e.g. *.xlsm). As a result, these files were often not accepted by customers from industry as their IT security system blocked the executions of macro code. With newer Excel versions (e.g. Excel 2021) you can create user-defined functions using Excel’s formula language, i.e. using the so-called LAMBDA function. I’ve tested the LAMBDA function with respect to its usability in the field of data analysis and I wanted to share my first experiences with you guys.
Creating a simple user-defined function
To get a bit comfortable with the LAMBDA function, let’s have a look at a very basic example. Say we want to “encode” the four parameter logistic (4PL) function that is often used for the curve fitting of ELISA-Assays or for logistic regression:
![]()
![]() has four input arguments: the lower asymptote
has four input arguments: the lower asymptote ![]() , the upper asymptote
, the upper asymptote ![]() , the Hill slope
, the Hill slope ![]() and the
and the ![]() -value where 50 percent of the signal is reached
-value where 50 percent of the signal is reached ![]() . Now let us start defining the corresponding
. Now let us start defining the corresponding LAMBDA function entering the following code into an Excel cell:
=LAMBDA(x,D,A,B,C,D+(A-D)/(1+EXP(B*LN(x)-C)))After hitting <Enter> you should have received a #CALC!error warning. No worries, this is not bad per se! It just means that although your LAMBDA function has five input arguments (x, D, A, B and C), you have not actually provided them (e.g. as concrete numbers). You could do so e.g. by adding the following inputs in brackets:
=LAMBDA(x,D,A,B,C,D+(A-D)/(1+EXP(B*LN(x)-C)))({0.000001,0.00001,0.0001,0.001,0.01,0.1},10,1,1,-4)Herein, the input ![]() is an array of 6 numbers ranging from
is an array of 6 numbers ranging from ![]() to
to ![]() . I entered concrete numbers here, but this could have been a range of the same numbers defined in some cells, too. The second to fifth inputs are single numbers. When you hit <Enter>, the output should be an array of the same size as
. I entered concrete numbers here, but this could have been a range of the same numbers defined in some cells, too. The second to fifth inputs are single numbers. When you hit <Enter>, the output should be an array of the same size as ![]() . Now we make this function generally available in the Excel workbook at hand and assign it the name
. Now we make this function generally available in the Excel workbook at hand and assign it the name FourPL. Therefore, copy this part
=LAMBDA(x,D,A,B,C,D+(A-D)/(1+EXP(B*LN(x)-C)))and go to Formulas and open the Name Manager. Click on New... to assign the aforementioned Name. You might change the Scope (which we will not do here). Add a comment, e.g. to explain the different input arguments and the function outputs. Finally, paste the LAMBDA function into the Refers to field. Clicking OK will finish the process. Close the Name Manager again and you can try using the FourPL function in an Excel cell. After typing Four into a cell, Excel should already suggest the FourPL function.
Creating a more advanced user-defined function for linear regression
In the previous section we used the LAMBDA function to add a 4PL function to our Excel function repertoire. Now we are going to define a user-defined function for the estimation of the coefficients of a linear regression calculation in preparation for the iteratively reweighted least-square (IRLS) regression described at the end of this post. Let’s shortly recapitulate the matrix notation of linear regression:
![]()
Herein, ![]() denotes the vector of responses (e.g. absorbance signal).
denotes the vector of responses (e.g. absorbance signal). ![]() denotes the design or Jacobi matrix and
denotes the design or Jacobi matrix and ![]() denotes the vector of regression coefficients.
denotes the vector of regression coefficients. ![]() denotes the residuals (that are assumed to be normally distributed with mean 0 and variance
denotes the residuals (that are assumed to be normally distributed with mean 0 and variance ![]() ). Linear regression minimizes the sum of the squared residuals
). Linear regression minimizes the sum of the squared residuals ![]() . After differentiation (with repect to
. After differentiation (with repect to ![]() ) and setting the resulting equation to zero, we finally end-up with the following matrix equation:
) and setting the resulting equation to zero, we finally end-up with the following matrix equation:
![]()
This last formula is exactly what we are going to store in a user-defined function. We’ll call it
LinReg. Let us first think about the in- and outputs to this function. The user shall input the design Matrix LinReg then returns the coefficient vector LAMBDA function contains array functions such as MMULT and TRANSPOSE:=LAMBDA(X,y,MMULT(MINVERSE(MMULT(TRANSPOSE(X),X)),MMULT(TRANSPOSE(X),y)))To test the LAMBDA function you may enter concrete arrays for ![]() and
and ![]() . For instance, say we obtained the following aborbance measurements in the lab:
. For instance, say we obtained the following aborbance measurements in the lab:
| Concentration values | Absorbance values |
| 0.05 | 0.572 |
| 0.55 | 1.241 |
| 1.05 | 2.215 |
| 1.55 | 2.175 |
| 2.05 | 3.308 |
Then the design matrix is:
![Rendered by QuickLaTeX.com \[\mathbf{X} = \begin{bmatrix}1 & 0.05\\1 & 0.55\\1 & 1.05\\1 & 1.55\\1 & 2.05\end{bmatrix}\]](https://dataanalysistools.de/wp-content/ql-cache/quicklatex.com-fb99ddfe41e4d6ceb6202f2e871f24ec_l3.png)
which needs to be available as a corresponding range in Excel (say E2:F6). ![]() is simply the vector of the absorbance values and must also be available as a dedicated range in Excel (say
is simply the vector of the absorbance values and must also be available as a dedicated range in Excel (say C2:C6). Then you can test the above LAMBDA function by inputting these ranges:
=LAMBDA(X,y,MMULT(MINVERSE(MMULT(TRANSPOSE(X),X)),MMULT(TRANSPOSE(X),y)))(E2:F6,C2:C6)The result vector ![]() should be
should be ![]()
Finally, you can again go to the Name Manager under Formulas and assign the function name LinReg so this function becomes available for calculation as any other conventional Excel function.
Recursive LAMBDA functions
Here is where I think that the LAMBDA has a great potential to replace VBA-code. You can use LAMBDA functions in a recursive manner. What does that mean? The LAMBDA function calls itself inside the body of the function definition. That sounds a bit abstract. So let’s make a simple example from maths. The factorial of a non-negative integer ![]() is defined by
is defined by
![]()
By definition, 0! is equal to 1. The factorial of 5 is ![]() . Although Excel already has a built-in function to calculate the factorial, namely
. Although Excel already has a built-in function to calculate the factorial, namely FACT, we want to create a custom function FACTORIAL that calculates exactly the same as FACT and thus learn what recursive LAMBDA function actually means. Here is how you do it:
=LAMBDA(n,IF(n<=1,1,FACTORIAL(n-1)*n))If you type this into a cell in Excel you get again the #CALC! error that we already know. However, even if you pass 5 as input
=LAMBDA(n,IF(n<=1,1,FACTORIAL(n-1)*n))(5)you will not succeed and get a #NAME? error as the expression FACTORIAL is unknown to Excel. Before we look closer at the functional expression, you must first acquaint Excel with that FACTORIAL function. Therefore, copy the above expression (without the input 5 in brackets) and go to FORMULAS and to NAME MANAGER to create a NEW... user-defined function. Paste the expression in the Refers to: text box and assign FACTORIAL as Name. Now the above test expression with 5 as an input should return 120 in the corresponding cell. But how does the function actually work? Let’s use our fiver example to step through the function. When inputting ![]() into the above function, the IF-statement will first be false and thus the actually recursive part,
into the above function, the IF-statement will first be false and thus the actually recursive part, FACTORIAL(n-1)*n will be executed. Plugging in the concrete numbers: FACTORIAL(4)*5 is what is calculated. In the next step the FACTORIAL function will again be passed with ![]() (first part), so that we get
(first part), so that we get FACTORIAL(3)*4 and in total FACTORIAL(3)*4*5. The moment ![]() becomes smaller or equal to 1, the if statement becomes true and the function leaves the recursive part to return a 1 only. The IF-statment in the
becomes smaller or equal to 1, the if statement becomes true and the function leaves the recursive part to return a 1 only. The IF-statment in the LAMBDA definition is very important since otherwise function executions do not stop and Excel gets stuck in a never-ending loop. When everything works at the end, you should receive 120 for an input of 5 to the FACTORIAL function. Comparing this to Excel’s internal function FACT, reveals the correctness of our user-defined FACTORIAL function.
Now let us come to a more practical example for recursive LAMBDA function to be used in data analysis.
Calculating the Wilcoxon-Mann-Whitney U statistic using a recursive LAMBDA function
The Mann-Whitney U-test is a famous non-parametric hypothesis test to, loosely said, compare the medians of two data groups. It is actually the non-parametric pendant to the even more famous Student t-test being used to compare the means of two data groups. Compared to the Student t-test, the Mann-Whitney U-test does not make any assumption about the underlying distribution of the data. It is not my intention to go too much into detail about this test here (this is probably going to be a saparate post). Just to mention that there is one important recursive equation derived in the original paper written by Mann and Whitney to calculate the p-value corresponding to the test statistic ![]() calculated as the minimum of
calculated as the minimum of ![]() and
and ![]() :
:
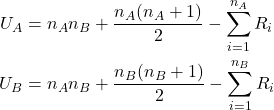
Herein, ![]() and
and ![]() denote the number of data points in group
denote the number of data points in group ![]() and
and ![]() , respectively.
, respectively. ![]() denotes the sum of ranks.
denotes the sum of ranks.
The recursion formula from the Mann and Whitney paper is now as follows:
![]()
![]() then denotes the aforementioned test statistic, i.e.
then denotes the aforementioned test statistic, i.e. ![]() . In the recursion formula,
. In the recursion formula, ![]() and
and ![]() can be viewed as running indices,
can be viewed as running indices, ![]() where
where ![]() and
and ![]() run from 0 to
run from 0 to ![]() and
and ![]() , respectively. As shown in their paper, Mann and Whitney state the following “constraints”:
, respectively. As shown in their paper, Mann and Whitney state the following “constraints”: ![]() if
if ![]() and also that
and also that ![]() are either zero or one depending on whether
are either zero or one depending on whether ![]() or
or ![]() . These constraints have caused me to split the task into two
. These constraints have caused me to split the task into two LAMBDA functions, i.e. one to calculate the ![]() -value (called
-value (called PU) incorporating the constraints and one to represent the actual recursion formula from above (we’ll call it MWUPVAL).
Below the definition of the LAMBDA function PU:
=LAMBDA(u,na,nb,IF(OR(u<0,u>na*nb),0,IF(OR(na=0,nb=0),IF(u<>0,0,1),IF(AND(na>0,nb>0),(na*PU(u,na-1,nb)+nb*PU(u-na,na,nb-1))/(na+nb)))))Make sure to assign this LAMBDA function the name PU using Name Manager in Excel. The second LAMBDA function MWUPVAL is then as follows:
=LAMBDA(u,na,nb,IF(u<0,0,MWUPVAL(u-1,na,nb)+PU(u,na,nb)))Note that this second LAMBDA function calls the first LAMBDA function PU. Make sure to assign this second LAMBDA function the name MWUPVAL using the Name Manger in Excel.
Finally, you might try the MWUPVAL function on the data set below:
| Data group A (Rank) | Data group B (Rank) |
| 54 (8) | 42 (4) |
| 23 (1) | 34 (2) |
| 45 (5) | 65 (9) |
| 53 (7) | 77 (11) |
| 41 (3) | 46 (6) |
| 73 (10) |
I’ve written the ranks in brackets corresponding to the measurement values in the table. Herein ![]() ,
, ![]() and
and ![]() ,
, ![]() . Thus,
. Thus, ![]() is equal to 13. Using
is equal to 13. Using MWUPVAL(13,6,5) finally calculates the corresponding (one-sided) p-value of 0.396 which is rather big indicating that the two group medians are not significantly different (based on a significance level of ![]() ).
).
Please note that I tried to keep the section about the Mann-Whitney U-test short as this might be detailed later in a dedicated blog post. Here I just wanted to give you a (admittedly rather complex) example for a recursive LAMBDA function. So please don’t resent me if not everything was immediately obvious!
Reference
H. B. Mann, D. R. Whitney. “On a Test of Whether one of Two Random Variables is Stochastically Larger
than the Other.” The Annals of Mathematical Statistics, 18(1) 50-60 March, 1947.
https://doi.org/10.1214/aoms/1177730491
Iteratively reweighted least-square (IRLS) using a recursive LAMBDA function
Now comes the surpreme discipline. We will combine the knowledge from the previous sections about linear regression in matrix form and about recursive LAMBDA functions to perform an iteratively reweighted least-square regression (IRLS). IRLS is often used with generalized linear models (GLM), such as with logistic regression. A conventional least-square regression is not appropriate in these cases as the pre-requisites of conventional least-square regression are violated (e.g. constant variance of the residuals). Thus, an appropriate weighting is required. The matrix equation that we are going to implement hence contains a weighting matrix ![]() that does not have fixed weighting coefficients but coefficients that are optimized within the least-square procedure:
that does not have fixed weighting coefficients but coefficients that are optimized within the least-square procedure:
![]()
E.g. in practice, it can occur that the scatter increases with increasing response values (e.g. often seen with ELISA readouts). To account for that ![]() is a common weighting scheme used in these cases. Remembering that
is a common weighting scheme used in these cases. Remembering that ![]() the above equation becomes recursive:
the above equation becomes recursive:
![]()
In contrast to conventional weighted least-square regression the above equation is calculated in an iterative manner.
Now let us implement this as a
LAMBDA function in Excel:=LAMBDA(i,X,b,y,IF(i<=1,b,MMULT(MINVERSE(MMULT(TRANSPOSE(X),MMULT(MUNIT(COUNT(y))1/(MMULT(X,WLINREG(i-1,X,b;y)))^2,X))),MMULT(TRANSPOSE(X),MMULT(MUNIT(COUNT(y))1/(MMULT(X,WLINREG(i-1,X,b,y)))^2,y)))))The input to this function contains the maximum number of iterations ![]() , the design matrix
, the design matrix ![]() and
and ![]() denoting the initial guess vector and
denoting the initial guess vector and ![]() the vector of responses. I do not want to go into the details of this function, but again you might recognize the IF-statement to ensure that the iteration fades out when approaching 1. In practice, iterations are stopped when the
the vector of responses. I do not want to go into the details of this function, but again you might recognize the IF-statement to ensure that the iteration fades out when approaching 1. In practice, iterations are stopped when the ![]() -value of two successive iterations are indistinguishable to some degree of (predefined) tolerance. However, this would have made the
-value of two successive iterations are indistinguishable to some degree of (predefined) tolerance. However, this would have made the LAMBDA function expression even more complicated and so I simply limited the number of iterations using the parameter ![]() .
. MINVERSE, MMULT, MUNIT and TRANSPOSE are standard Excel array functions. WLINREG, however, is the name of the user-defined function that I assigned at the end to the above LAMBDA-function. Using WLINREG with the data from section 2 and with ![]() ,
, ![]() and the same design matrix
and the same design matrix ![]() as in section 2, you should get
as in section 2, you should get ![]() for
for ![]() which is slightly different from what we obtained for the conventional (non-weighted) linear regression.
which is slightly different from what we obtained for the conventional (non-weighted) linear regression.
Please note that the number of recursions currently seems quite limited in Excel. E.g. when I try ![]() with the
with the WLINREG function, Excel is working quite hardly but returns 0 at the end. Not sure, but also the number of executable recursions seems to depend on the number of function evaluations inside the LAMBDA function. And as our LAMBDA function has quite a lot of functions (including all the array functions), the number of recursions seems limited.
There are currently other limitations for LAMBDA functions. One of the most obvious ones is that its use is limited to the current Excel workbook. That means a user-defined LAMBDA function is unfortunately not available in other Excel workbooks.
Another issue is that LAMBDA functions are not backward compatible, e.g. if you open an Excel workbook in Excel 2016 that had been created with Excel 2021, the numbers of the LAMBDA function might be displayed first, but when you edit the cell the corresponding cell will return an error afterwards.