A non-parametric analysis to determine the ED50, SD50 or similar metrics
The first time I came across the term Spearman-Kärber was with the analysis of RT-QuIC. These assays are typically used to detect small amounts of prions, i.e. proteins that can induce conformational changes in other proteins and lead to diseases like Creutzfeldt-Jakob disease. A short-hand notation for prion protein that is often used is PrP. In an RT-QuIC assay a liquid body sample (e.g. cerebrospinal fluid) supposed to contain infectious PrPI is diluted with native-conformation-PrPC. The dilution series is typically performed on a logarithmic scale while keeping the concentration of diluent (PrPC solution) constant. Each dilution series is replicated several times and each sample of this series is applied to vigorous shaking typically in a microplate reader capable of detecting Thioflavin T (ThT) fluorescence. Thioflavin T is a fluorescence dye that becomes fluorescent when bound to aggregated PrPI. Thus, the time course of aggregation can be monitored with ThT. If PrPI were present in the original sample at high concentration one would observe an increase of the fluorescence over time. At high concentrations of PrPI all replicates will start aggregating at some point, while for more diluted samples only a portion of the replicates will aggregate (in a given time period). At the highest dilution there is likely to be no aggregation at all. Plotting the portion of aggregated replicates as a function of dilution often gives a sigmoidal curve going from 0 (no replicate was positive /aggregated) to 1 (all replicates were positive /aggregated). There are various ways how to analyze such data. But one of the most common ways is to perform a Spearman-Kärber analysis. It is a general non-parametric way to estimate the mean effective seeding dose SD50, mean lethal dose, mean effective dose or some other mean EX50 quantity and its corresponding error.
If the aforementioned portions pi were plotted as a function of the seeding dilution, the graph would be the empirical estimate of the cumulative distribution function F(x) of the underlying (continuous) distribution. It is often referred to as tolerance distribution whose probability distribution function shall be denoted with f(x). For the continuous case, f(x) can be obtained by differentiating F(x) with respect to x (since F(x) is an integral of f(x)). Although the tolerance distribution is continuous, we can approximate it by the discrete empirical cumulative distribution function F(x). In the discrete case, f(x) (I should rather write f(xi) can be obtained by differencing F(x), i.e. F(xi+1)- F(xi). Herein x denotes the log(dilution) or log(dose). In formal terms what was said means: If we were to estimate the mean of the log(dose) we use the general formula for the mean of a discrete random variable:
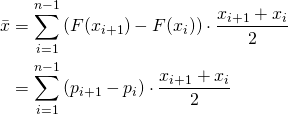
The term ![]() takes into account that we approximate the continuous tolerance distribution by an empirical with only discrete base points
takes into account that we approximate the continuous tolerance distribution by an empirical with only discrete base points ![]() . For more details refer to Spearman’s publication. The summation in the equation is over all doses assuming that there is no response for any of the replicates at the lowest dose
. For more details refer to Spearman’s publication. The summation in the equation is over all doses assuming that there is no response for any of the replicates at the lowest dose ![]() (i.e.
(i.e. ![]() ) and that all replicates are positive at the highest dose
) and that all replicates are positive at the highest dose ![]() , i.e.
, i.e. ![]() . If this is not given by the experimental data, one can introduce fake data points. Say
. If this is not given by the experimental data, one can introduce fake data points. Say ![]() , then one can introduce a fake dose
, then one can introduce a fake dose ![]() and set
and set ![]() . But how to set
. But how to set ![]() ? If the
? If the ![]() ’s are evenly spaced (which is often the case) one can simply subtract the constant
’s are evenly spaced (which is often the case) one can simply subtract the constant ![]() from
from ![]() to end-up with
to end-up with ![]() , i.e.
, i.e.
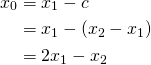
On the other hand, if ![]() , a fake dose
, a fake dose ![]() can be calculated by:
can be calculated by:
![]()
One can try using these types of fake doses even if the experimental doses are not evenly spaced. Please note that if the fake doses are taken into account, the lower and upper limit of summation in the equation for ![]() will change.
will change.
The standard error ![]() of the mean can be calculated by a simple equation:
of the mean can be calculated by a simple equation:
![Rendered by QuickLaTeX.com \[ s=\frac{1}{2}\sqrt{ \sum_{i=1}^{n}\left(x_{i-1}+x_{i+1} \right)^2 \frac{p_i (1-p_i)}{n_i-1}}\]](https://dataanalysistools.de/wp-content/ql-cache/quicklatex.com-ab97c0fbcc71744d27b18109193a9fe3_l3.png)
The standard error can then be used to calculate an (1-α)-percent confidence interval:
![]()
Where ![]() denotes the
denotes the ![]() -quantile of the Student t-distribution.
-quantile of the Student t-distribution.
Although it might seem complicated at first glance, the Spearman-Kärber formula is supposed to be calulable by hand and without the need for fitting etc. There are other methods like the Reed-Muench or Dragestedt-Behrens aiming at a similar goal of being easily calculable. While this argument might have been a valid one at the time when the authors published their work, it might not be so important nowadays, as more complex methods like probit regression can be easily done by computers.
While the “classical” Spearman-Kärber (SK) analysis works nicely in many practical cases, state-of-the-art is the so-called trimmed Spearman-Kärber analysis as developed by Hamilton et al. It adds a trimming and scaling procedure before calculating the estimate for the median effective dose. Trimming is done in as much the same way as a the trimmed mean is calculated, i.e. a user-defined fraction (the trim) of the data is removed from the upper and lower end. However, I will not go to much into the details here. In the trimmed SK analysis, you need to set a trim value ![]() in the range from 0-0.5 and subsequently only
in the range from 0-0.5 and subsequently only ![]() percent of the data are finally used for calculating the mean effective seeding dose. In essence, the upper and lower
percent of the data are finally used for calculating the mean effective seeding dose. In essence, the upper and lower ![]() percent of the dose-response curve are cut-off. With this, one can get more robust estimates of the mean effective seeding dose as the heads and tails of the dose-response curve tend to be more prone to variations.
percent of the dose-response curve are cut-off. With this, one can get more robust estimates of the mean effective seeding dose as the heads and tails of the dose-response curve tend to be more prone to variations.
Thus, it becomes obvious that the “classical” SK analysis is a special case of the trimmed SK analysis with ![]() set to zero.
set to zero.
I created a simple Excel-sheet in order to demonstrate the calculations for the Spearman-Kärber analysis. Feel free to download and to paste your data into the appropriate table and run the analysis (no macros required).
I also created an Excel-sheet for the trimmed Spearman-Kärber which is available upon request from the author.
References
D. J. Finney, Statistical Method in Biological Assay, Hafner, 1952.
C. Spearman, “The Method of “Right and Wrong Cases” (Constant Stimuli) without Gauss’s Formula.,” British Journal of Psychology, p. 227–242, 1908.
G. Kärber, “Beitrag zur kollektiven Behandlung pharmakologischer Reihenversuche,” Archiv für experimentelle Pathologie und Pharmakologie, pp. 480-483, 1931.
M. A. Hamilton, R. C. Russo and R. V. Thurston, “Trimmed Spearman-Karber method for estimating median lethal concentrations in toxicity bioassays,” Environmental Science & Technology, p. 714–719, 1977. DOI: https://doi.org/10.1021/es60130a004.

